Generalized polygamma function

In mathematics, the generalized polygamma function or balanced negapolygamma function is a function introduced by Olivier Espinosa and Victor H. Moll.^[1] It generalizes the polygamma function to negative and fractional order, but remains equal to it for integer positive orders.

It is defined as follows:

$\psi(z,q)=\frac{\zeta'(z%2B1,q)%2B(\psi(-z)%2B\gamma ) \zeta (z%2B1,q)}{\Gamma (-z)} \,$

or alternatively,

$\psi(z,q)=e^{- \gamma z}\frac{\partial}{\partial z}\left(e^{\gamma z}\frac{\zeta(z%2B1,q)}{\Gamma(-z)}\right)$

Several special functions can be expressed in terms of generalized polygamma function.

$\psi(x)=\psi(0,x)\,$

$\psi^{(n)}(x)=\psi(n,x)\,\,\,(n\in\mathbb{N})$

$\Gamma(x)=e^{\psi(-1,x)%2B\frac 12 \ln(2\pi)}\,\,\,$

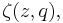$\zeta(z,q)=\frac{\Gamma (1-z) \left(2^{-z} \left(\psi \left(z-1,\frac{q}{2}%2B\frac{1}{2}\right)%2B\psi \left(z-1,\frac{q}{2}\right)\right)-\psi(z-1,q)\right)}{\ln(2)}$

where $\zeta(z,q),$ is the Hurwitz zeta function

$B_n(q) = -\frac{\Gamma (n%2B1) \left(2^{n-1} \left(\psi\left(-n,\frac{q}{2}%2B\frac{1}{2}\right)%2B\psi\left(-n,\frac{q}{2}\right)\right)-\psi(-n,q)\right)}{\ln (2)}$

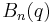where $B_n(q)$ are Bernoulli polynomials

$K(z)=A e^{\psi(-2,z)%2B\frac{z^2-z}{2}}$

where K(z) is K-function and A is Glaisher constant, which itself can be expressed in terms of generalized polygamma function:

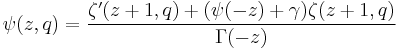
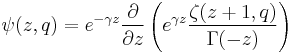
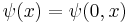
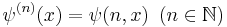
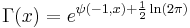
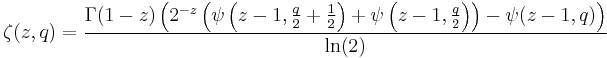
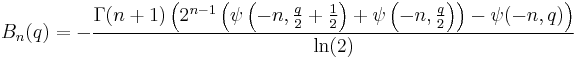
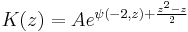
$A =\frac{\sqrt[36]{128{\pi}^{30}}}{\pi}e^{\frac{1}{3}%2B\frac{2}{3}\psi(-2,\frac 12)-\frac 13\ln(2\pi)}$

References

^ Olivier Espinosa Victor H. Moll. A Generalized polygamma function. Integral Transforms and Special Functions Vol. 15, No. 2, April 2004, pp. 101–115